---

Nggak kerasa sekarang udah 2024. Baru aja kemarin aku persiapin diri buat menjalankan resolusi tahun baru, eh, sekarang harus udah ngesiapin resolusi baru lagi nih.

Kayaknya makin kesini tuh makin nggak kerasa kalo waktu bergulir begitu cepat. Jadi pengen gitu cari cara supaya aku bisa keep track dengan jalannya waktu.

Oleh karena itu aku memulai baca-baca sedikit tentang sejarah waktu. Aku ingin belajar bareng kalian dan menenangkan kekhawatiranku bahwa memang sepanjang sejarah manusia, semua telah susah payah bergelut menjaga waktu.

Disini aku ingin memulai dengan salah satu penjaga waktu kita yang klasik dan simpel, pendulum.

---

Dimulai dari abad pej(el)ajahan

Untuk melihat awal mula penggunaan pendulum, aku ingin membawa kalian kembali ke abad ke-\(17\). Kita sekarang berada di Abad Penjelajahan, ribuan kapal meninggalkan pelabuhan Eropa demi mencari jalur-jalur perdagangan baru.

Menelusuri bumi di abad ini sayangnya nggak mudah, peta dunia aja masih belum lengkap, apalagi GPS atau Google Map.

Bayangin aja, kamu ditelantarin di tengah laut tanpa peta, landmark, ataupun petunjuk apapun di sepanjang cakrawala. Jadi sangat krusial buat kita untuk mengetahui posisi kita biar nggak gampang nyasar.

Navigasi langit

Salah satu cara untuk melakukan itu adalah dengan menggunakan bintang, untuk menentukan garis lintang dan garis bujur.

Biasanya untuk garis lintang, kita bisa menentukannya dari posisi tertinggi matahari relatif ke garis ufuk. Semakin tinggi posisi matahari, semakin dekat kita ke garis khatulistiwa.

Di malam hari, kita juga bisa mengukur posisi garis lintang menggunakan posisi bintang. Contohnya, kalo kita berada di belahan utara Bumi, kita bisa menggunakan bintang Polaris, yang terletak persis di garis sumbu rotasi Bumi. Kebalikan dengan matahari, semakin tinggi posisi Polaris, semakin jauh kita dari garis khatulistiwa.

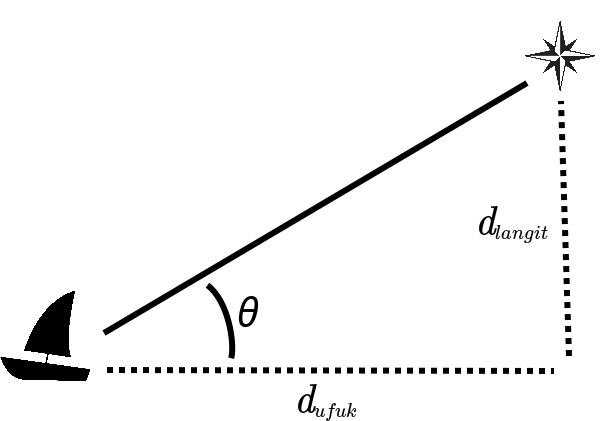
Dengan penjabaran trigonometri diatas, kita bisa menemukan posisi garis lintang dari ketinggian bintang Polaris dengan rumus

\[\tan{\theta_{\text{g-l}}}=\frac{d_\text{langit}}{d_\text{ufuk}}.\]

Nah… kalo garis bujur beda lagi caranya. Disini kita bisa lihat pergantian posisi sudut bintang di waktu yang sama. Jumlah pergantian posisi sudut di bintang \(\Delta\theta\) tersebut sesuai dengan jumlah perubahan garis bujur atau garis bujur relatif yang kita tempuh \(-\Delta\theta\), seperti yang ada di gambar berikut:

Sayangnya, kalkulasinya biasanya kurang akurat karena sewaktu itu biasanya menggunakan tabel waktu berdasarkan posisi Polaris dan matematikanya pun terlalu rumit untuk pelaut pada umumnya ¹.

Oleh karena itu, dibutuhkanlah cara untuk mencari posisi garis bujur secara simpel dan akurat.

Menerka ruang melalui waktu

Jadi gimana cara kita menghitung garis bujur dengan simpel dan akurat? Kita lakukan itu dengan jam. Dengan memiliki jam di kapalmu, nggak hanya kamu bisa mengukur garis bujur relatif tanpa harus menggunakan tabel waktu dan Polaris, tapi kamu juga bisa menghitung betul posisi absolut garis bujur.

Ini bisa dilakukan menggunakan jam. Dengan membawa jam yang memantau waktu pada tempat asalmu, kamu bisa melihat berapa perbedaan waktu pada waktu lokal dan waktu di tempat asalmu. Disini, kita bisa menggunakan titik tertinggi matahari sebagai patokan jam \(12\) waktu lokal contohnya.

Karna kita tau bahwa satu kali rotasi bumi itu sama dengan \(24\) jam, kita jadinya tau berapa perubahan garis bujur yang telah kita tempuh dengan pergantian waktu yang kita alami.

Contohnya, kalau seharusnya kita tau bahwa waktu lokal seharusnya jam $12.00$, dan ternyata jam yang kita bawa menunjukan jam \(15.30\), berarti kita \(3.5\) jam lebih telat dan telah bergerak ke barat sepanjang \(\frac{3.5}{24}\) dari lingkar bumi.

Thanks to imperialism, kita bisa menghitung posisi garis bujur absolut \(\theta_\text{g-b}\) menggunakan waktu jam Greenwich \(T_\text{GMT}\) (GMT +00) saat matahari berada di titik tertinggi,

\[\theta_\text{g-b}=\frac{180^\circ}{12}(12.00-T_\text{GMT}).\]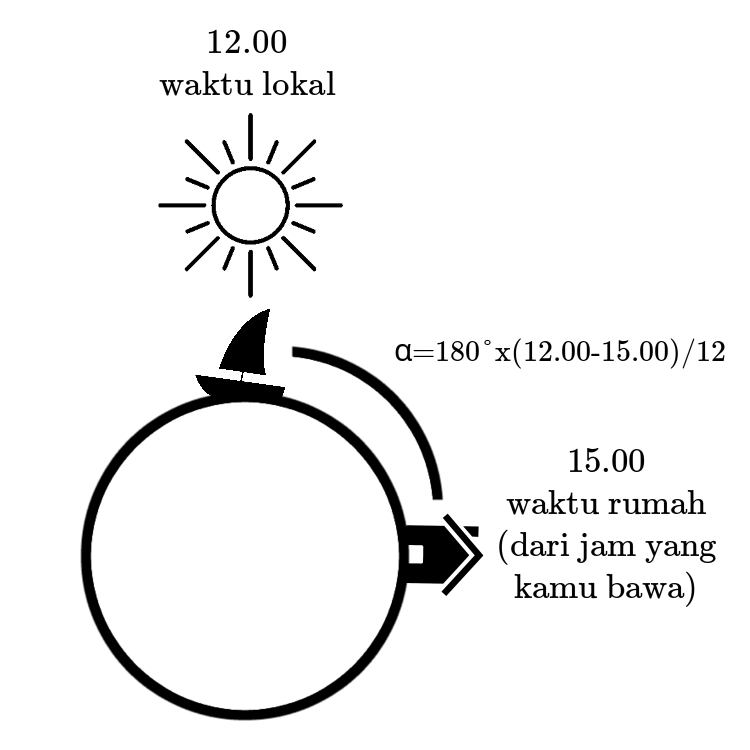

Terus apa yang menghentikan orang pada abad Penjelejahan untuk menggunakan metode diatas? Well, kita waktu dulu belum mempunyai jam kapal yang bisa menghitung detik secara akurat.

Jam sebenarnya sudah ada dari dulu. Kita sudah menggunakan jam matahari yang memakai posisi bayangan matahari, tapi sayangnya nggak bisa dipindahin. Jam pasir juga udah ada, bisa dibawa kemana-mana, tapi kurang akurat. Kita juga ada jam air yang akurat, tapi nggak praktis untuk dibawa di kapal.

Saking pentingnya mempunyai jam yang akurat, Dewan Negara Belanda (setara dengan DPR-nya Indonesia) menjanjikan bayaran sebesar \(10000\) florins pada tahun \(1627\) ², atau setara dengan $9$ milyar rupiah!

Dengan upah segitu menggiurkan, banyak saintis tergoda untuk memecahkan masalah ini, termasuk sang “bapak metode ilmiah dan ilmu fisika modern”, Galileo.

Awal mula pendulum

Sebelum masanya Galileo, aku ingin mengejutkan kalian dengan fakta bahwa penggunaan pendulum bukan sesuatu yang umum. Sebuah masa yang diikat ke tali dan dibiarkan bergerak tidak mempunyai manfaat atau kegunaan sesekalipun!

Studi yang melibatkan pendulum baru dimulai oleh Nicole Oresme pada tahun \(1350\), yang mendeskripsikan bahwa setiap benda memiliki sebuah impetus atau “dorongan”. Dia menunjukan bahwa kalo kita mengikat sebuah masa dengan tali, dan menjatuhkannya dari titik yang tinggi, masa itu akan mendapatkan sebuah dorongan untuk naik lagi keatas.

Oresme berpostulasi bahwa, kalo kita menjatuhkan sebuah masa ke lubang yang menembus bumi, masa tersebut akan melewati pusat bumi dan berhenti sedekat lebih pendek dari permukaan bumi. Masa tersebut kemudian akan jatuh lagi ke bawah menembus bumi dan keluar sedikit lebih pendek lagi dari tinggi lubang tempat kita menjatuhkan masa tersebut. Pada akhirnya, Oresme menyimpulkan bahwa masa tersebut akan kehilangan “dorongan” dan berhenti di pusat bumi ³.

Gedankenexperiment (kata Jerman dari eksperimen pikiran) diatas adalah deskripsi awal dari gerakan osilasi, atau gerakan berayun-ayun, yang menjadi ciri khas dari sebuah pendulum.

Sebuah revisi mekanika

Tentu saja sekarang kita sudah mengenal pergerakan osilasi yang disebut oleh Oresme sebagai bukti dari hukum gerak Newton ke-2 dan hukum kekekalan energi, namun perlu diingat bahwa hukum-hukum gerak Newton, baru hanya akan dinyatakan di Principia Mathematica yang diterbitkanpada tahun tahun \(1687\).

Terlepas dari itu, apa sih memang fisika dibalik sebuah pendulum?

Hukum mekanika

Untuk ngingetin, bahwa Hukum gerak ke-2 Newton berkata “pergantian momentum di sebuah benda berbanding lurus dengan total gaya yang diberikan di sebuah benda, \(\sum\vec F=\frac{d\vec p}{dt}\)“, dan hukum kekekalan energi berkata “energi tidak bisa dibuat atau dihancurkan, hanya diubah dari satu ke bentuk yang lain,\(\sum E =\sum E'\)“.

Well, pertama-tama impetus atau dorongan yang dicanangkan oleh Oresme tidak lain adalah momentum. Ketika pendulum dilepas dalam keadaan diam, pendulum tersebut tidak mempunyai momentum. Namun karena ada gaya, pendulum tersebut mengumpulkan momentum dan bergerak lagi keatas.

Gaya yang memicu pergantian momentum adalah gaya tarikan \(\vec T\) dan gaya gravitasi \(\vec F_g\), yang berarti

\[\vec T+\vec F_g = \frac{d\vec p}{dt}\]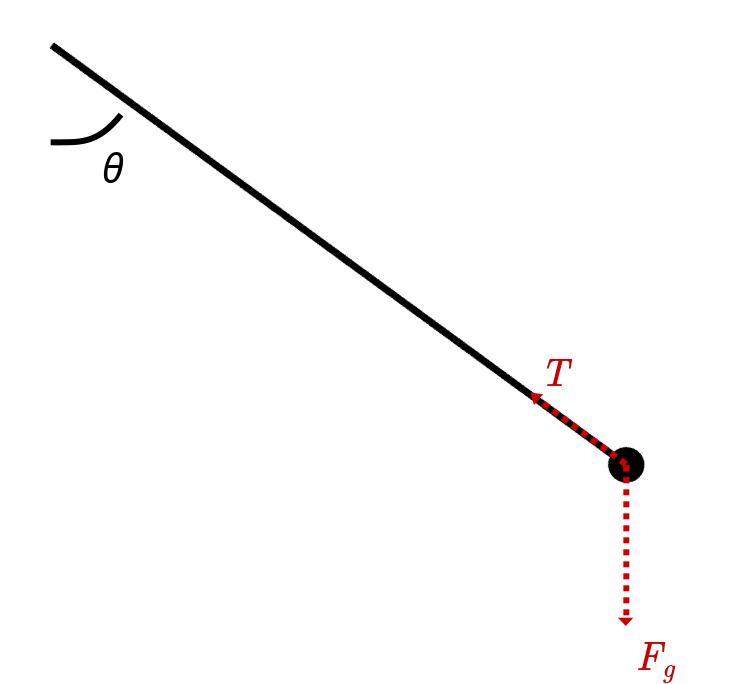

Di arah radial \(\vec e_r\) (yang berarah berlawanan dengan gaya tarikan), kita punya gaya tarikan \(\vec T\) yang mampu menyesuaikan ukurannya dengan kecepatan benda dan gaya gravitasi radial \(\vec F_{g,r}\) sehingga jumlahnya memberikan pergerakan lingkaran (gaya sentripetal)

\[\vec T + \vec F_{g,r}=(T+mg\cos\theta)\vec e_r= \frac {d\vec p_r}{dt} =\vec F_{cp}=-\frac{mv²}{r}\vec e_r.\]

Jadi kita tersisa dengan arah tangensial \(\vec e_\theta\) (yang searah dengan pergerakan masa pendulum, sepanjang lingkaran). Kita tahu bahwa kalau panjang dari pendulum adalah \(l\), posisi masa pendulum adalah \(l\theta\). Terlebih lagi, karena tidak ada pergerakan radial, kita bisa dengan mudah berasumsi bahwa semua percepatan hanya mengubah posisi sudut \(\theta\),

\[\vec F_{g,t}=mg\sin\theta\vec e_\theta=\frac{d\vec p_\theta}{dt}=m\frac{d\vec v_\theta}{dt}=ml\frac{d^2}{dt^2}(\theta )\vec e_\theta.\]

Terus dengan kekalan energi, kita bisa melihat bahwa ada dua jenis energi yang dimiliki sang pendulum. Energi potensial yang dimiliki saat pendulum itu bisa jatuh karena gravitasi, dan energi kinetik, atau energi gerak, yang didapatkan ketika energi potensial itu diubah menjadi sebuah gerakan yang mempunyai momentum. Karena tali dari pendulum itu menahan masa pendulum untuk turun lebih jauh, si pendulum-nya pun bisa menggunakan energi kinetik untuk kembali mengayun ke atas. Dengan begitu terjadi tarik-ulur antara keadaan energi kinetik dan energi potensial.⁴

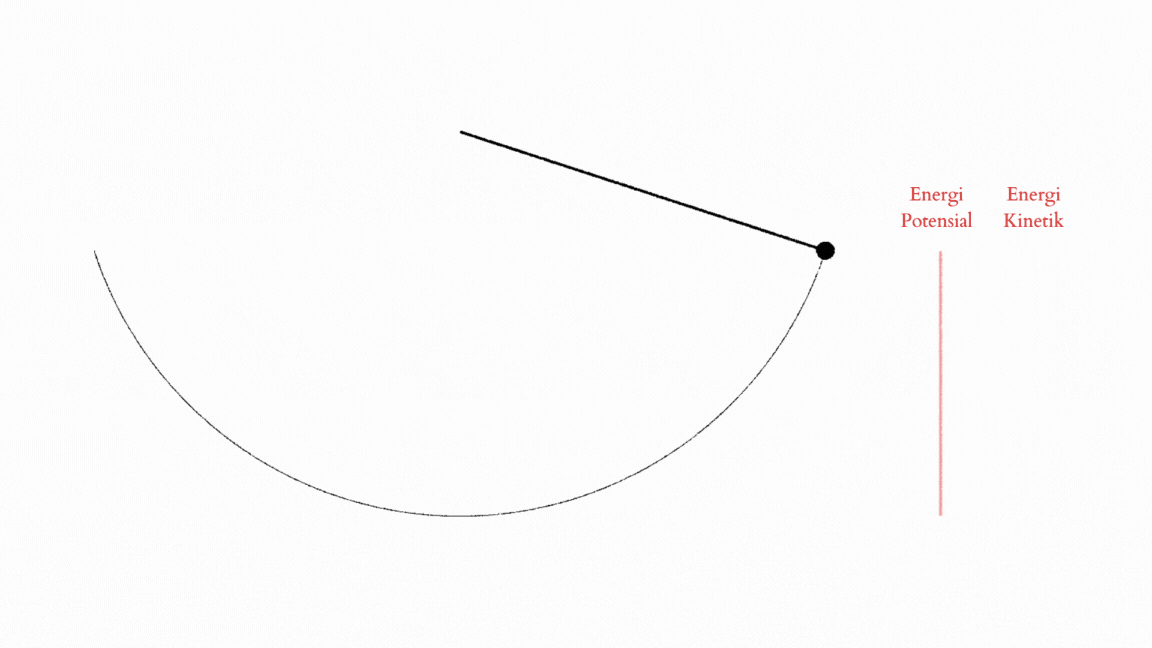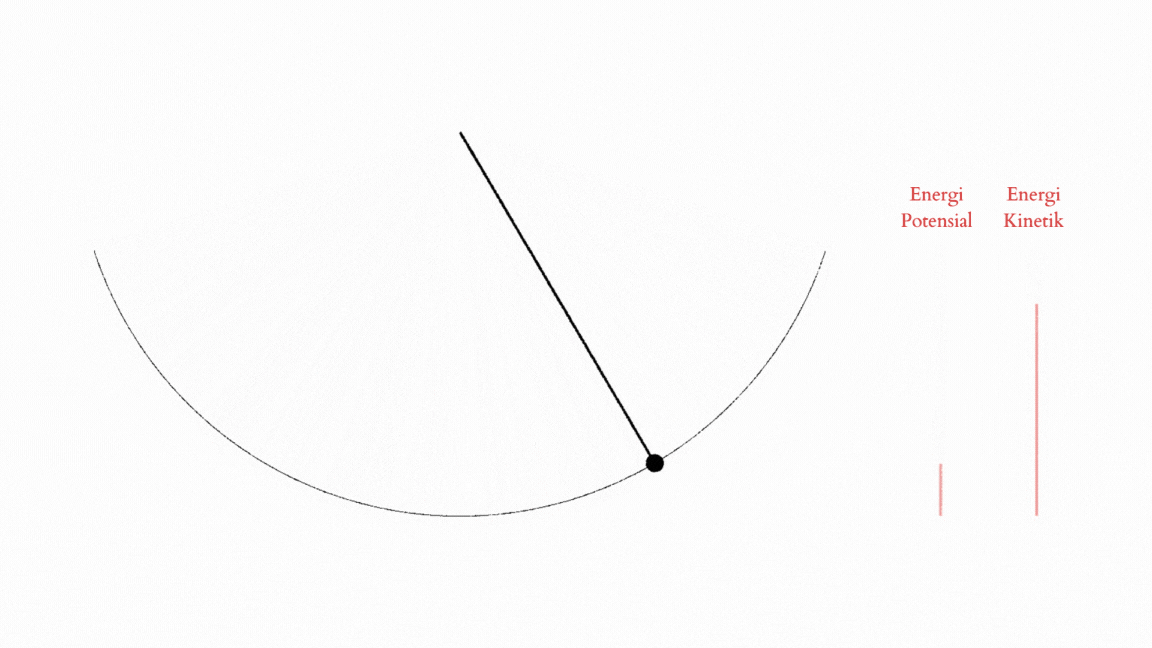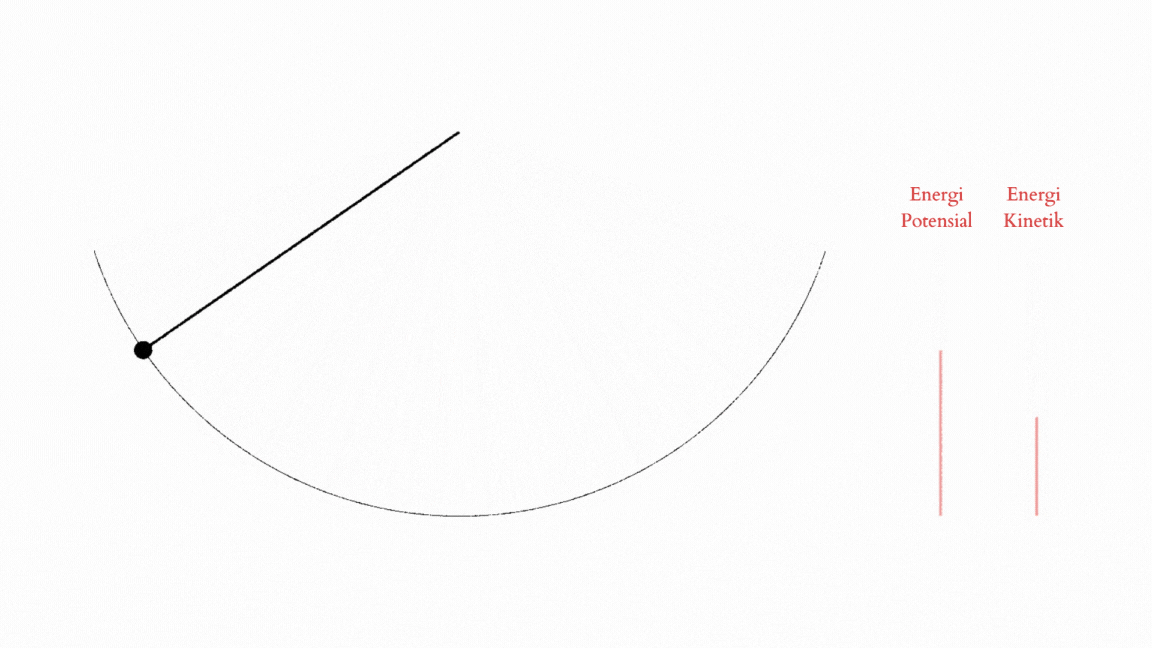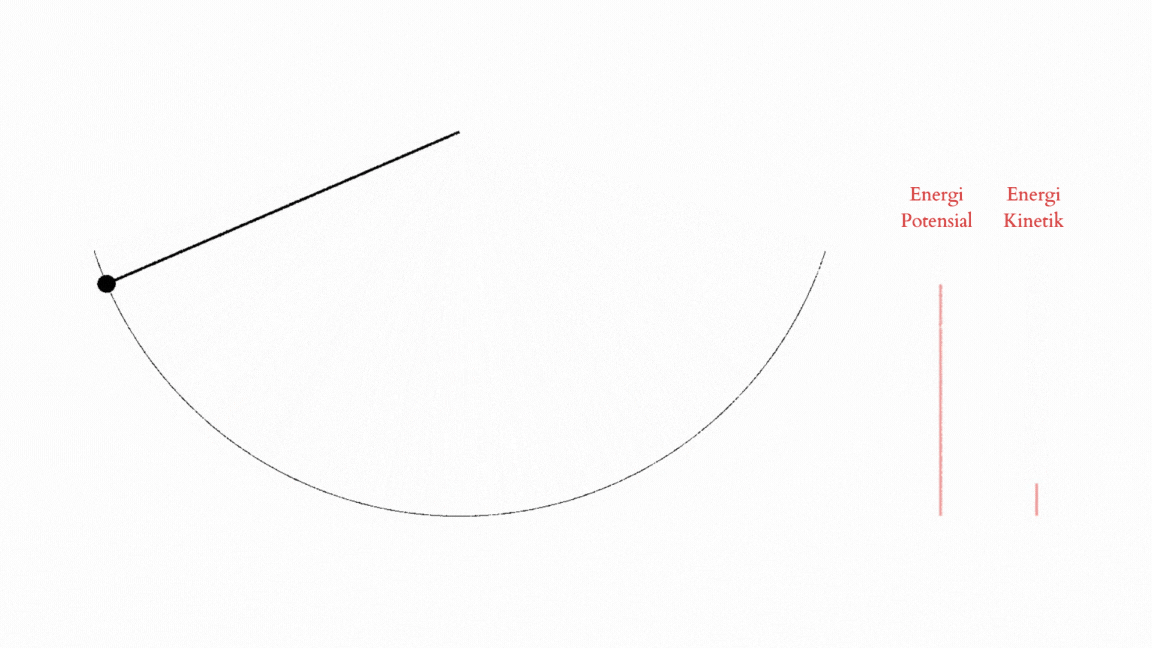
Kita bisa menulis total energi tersebut dengan formulasi standar (kiri) dan formulasi sudut (kanan),

\[E=mgh+\frac{1}{2}mv^2=mgl(1-\cos\theta)+\frac{1}{2}ml^2\left(\frac{d\theta}{dt}\right)^2.\]

Nah, with all the physics done, kita bisa lihat bahwa observasi oleh Oresme tentang pergerakan berayun ini benar-benar mendahului zamannya.

Sayangnya anggapan Oresme, bahwa impetus adalah sesuatu yang bisa menghilang (yang mungkin kita atribusi sekarang sebagai friksi) sehingga melihat pergerakan berayun-ayun tersebut sebahai sesuatu yang inkosisten dan tidak konstan, membuat dia kehilangan kesempatan menemukan manfaat dari pendulum.

Ritme yang mengubah segalanya

Studi tentang teori impetus-nya Oresme tidak pernah dikembangkan lagi oleh seseorang diluar lingkaran akademisi-nya. Semua studi tentang osilasi benar-benar redup hingga kita kembali ke Galileo. Terlepas dari hadiah uang yang dijanjikan pemerintah Belanda, Galileo sendiri memang juga mempunyai kepentingan tersindiri untuk menjaga waktu. Dia adalah seorang astronom.

Di astronomi, menjaga ketepatan waktu itu penting terlebih untuk melihat sebuah transit. Transit yang aku maksud disini bukan transit pesawat, melainkan momen ketika sebuah benda luar angkasa melewati depannya benda angkasa lainnya. Gerhana adalah contoh transit yang benar-benar bisa dilihat. Disini, Galileo mengincar sesuatu yang lebih sulit, yaitu transit bulan-bulan di Jupiter.

Untuk memecahkan masalah waktu, Galileo membuat sebuah observasi yang simpel, tapi cukup dahsyat. Konon katanya, ini berawal ketika Galileo datang ke Katedral Pisa dan melihat lampu yang berayun dengan ritme yang reguler. Seperti sebuah ilham yang ditujukan kepada Galileo, dia langsung bergegas mendesain sebuah alat pendulum yang bisa mengukur waktu ³.

Disclaimer

Sama hal-nya dengan semua cerita yang melibatkan Galileo dan 🍕. Ini semua dongeng yang dilempar dari ilmuwan ke ilmuwan.

Gimana Galileo bisa medesain pendulum yang bisa mengukur waktu? Well kita harus balik lagi ke fisika!

Berdasarkan hukum kekekalan energi, kita tahu bahwa energi awal di pendulum, yaitu ketika pendulum berhenti di atas, let’s say di sudut inisial \(\theta_0\), harus sesuai dengan total energi yang ada ketika pendulum bergerak di bawah. Berarti menggunakan rumus energi pendulum di bab sebelumnya kita punya

\[mgl(1-\cos\theta_0)+=mgl(1-\cos\theta)+\frac{1}{2}ml^2\left(\frac{d\theta}{dt}\right)^2.\]

Disclaimer

Disini akan ada sedikit matematika rumit, just bear with me. Skip aja beberapa baris kalau pusing.

Kita susun ulang rumusnya, kita punya

\[\frac{d\theta}{dt}=\sqrt{\frac{2g(\cos\theta-\cos\theta_0)}{l}}.\]

Kemudian kita mengintegrasi fungsi diatas, dari titik terendah hingga titik tertinggi pendulum, yang bisa ditempuh dengan \(\frac{1}{4}\) periode dari sebuah ayunan,

\[\int_0^\frac{T}{4}dt=\frac{T}{4}=\sqrt{\frac{l}{2g}}\int_0^{\theta_0}\frac{d\theta}{\sqrt{\cos\theta-\cos\theta_0}}.\]

Kemudian kita menggunakan identitas \(\cos(2x)=1-2\sin^2x\), dan beberapa faktorisasi,

\[\frac{T}{2}=\sqrt{\frac{l}{g}}\int_0^{\theta_0}\frac{d\theta}{\sin(\theta_0/2)\sqrt{1-\frac{\sin^2(\theta/2)}{\sin^2(\theta_0/2)}}}.\]

Menggunakan substitusi $\sin u = \sin(\theta/2)/\sin(\theta_0/2)$, kita mendapatkan integrand,

\[du \cos u = d\theta\frac{\cos(\theta/2)}{2\sin(\theta_0/2)}\]

yang lagi-lagi menggunakan identitas trigonometri \(\cos x=\sqrt(1-\sin^2x)\) dan susunan ulang mendapatkan,

\[d\theta\frac{1}{\sin(\theta_0/2)}=du \frac{ 2\cos u}{\sqrt{1-\sin^2(\theta_0/2)\sin^2u}}.\]

Memasukkan substitusi diatas ke integral, kita mendapatkan,

\[\frac{T}{4}=\sqrt{\frac{l}{g}}\int_0^{\frac{\pi}{2}}\frac{du}{\sqrt{1-\sin^2(\theta_0/2)\sin^2u}}.\]

Ini adalah integral elliptis. Ini bukan integral yang mudah untuk diselesaikan, tapi ada cara jitu yang biasanya dilakukan fisikawan (dan terlebih lagi insinyur), untuk memecahkan masalah rumit seperti ini, Taylor S ⁵!

Eitsss, tunggu dulu, yang aku maksud bukan si penyanyi lagu Blank Space, Taylor Swift, tapi Taylor Series atau deretan Taylor. Menggunakan teorema Taylor itu salah satu hal favorit yang aku lakukan, dan juga tanpa aku sangka masih berguna walaupun aku sekarang kuliah matematika terapan!

Teorema Taylor

Jadi teorema ini mengatakan bahwa setiap fungsi matematika, dari fungsi transidental (yaitu rumit yang tidak bisa ditulis secara aljabar seperti \(e^x\) , \(\sin x\), dan \(\cos x\)) ke fungsi aljabar (yaitu sisanya, \(\frac{1}{x}\), \(\frac{\sqrt{1-x²}}{2x}\), dll.) bisa ditulis dengan deretan fungsi polynom yang didefinisikan oleh turunan-turunan fungsi itu sendiri!

Secara formal didefinisikan sebagai,

\[f(x)=f(a)+\frac{f'(a)}{1!}(x-a)+\frac{f^{(2)}(a)}{2!}(x-a)^2+\dots\]

dimana \(a\) adalah titik ekspansi dan ada nilainya untuk fungsi \(f\) dan semua turunannya.

Jadi apa manfaat dari teorema ini? Kalo kamu lihat setiap bagian dari deretan terikat dengan lipatan pangkat dari \((x-a)\). Jadi bayangin kalo \(x\) itu deket dari \(a\) sehingga \((x-a)=0.1\). Jadinya \((x-a)^2=0.01\), \((x-a)^3=0.001\), dst. Angkanya akan semakin mengecil!

Berarti kontribusi dari pangkat yang besar bisa dibilang sangat kecil! Seumpama ada fungsi yang rumit untuk kita komputasi (seperti di integral), kita bisa pakai teorema Taylor untuk hanya menggunakan beberapa angka pertama dari deretan Taylor, dengan syarat \(x\) dekat dari titik ekspansi \(a\).

Disini aku ingin menggunakan deretan Taylor untuk mendapatkan aproksimasi dari fungsi

\[\frac{1}{\sqrt{1-\sin^2(\theta_0/2)\sin^2u}}\]

untuk \(\theta_0\) di titik ekspansi \(0\).

Oke, untuk penjumlahan pertama, itu gampang, \(f(0)=\frac{1}{\sqrt{1-\sin^2(0)\sin^2u}}=1\).

Lanjut ke turunan kedua,

\[f'(0)=\frac{\sin(0)\cos(0)}{2\left(1-\sin^2(0)\sin^2u\right)^{\frac{3}{2}}}=0\]

jadi angka kedua di deretan Taylor kita juga menghilang.

Kita bisa lanjut ke turunan selanjutnya, tapi karena ini sudah pangkat ke-\(2\) dari \((\theta_0-0)\), asal aku memilih \(\theta_0\) yang dekat dengan \(0\), seharusnya kita aman.

Jadi dengan deretan Taylor, aku menyimpulkan bahwa fungsi diawal bisa diaproksimasi dengan

\[\frac{1}{\sqrt{1-\sin^2(\theta_0/2)\sin^2u}}=1+0+\dots\approx1.\]

Dengan ini, integral elliptis yang tadi kita harus kita selesaikan berubah menjadi

\[\frac{T}{4}=\sqrt{\frac{l}{g}}\int_0^{\frac{\pi}{2}}\frac{du}{\sqrt{1-\sin^2(\theta_0/2)\sin^2u}}\approx\sqrt{\frac{l}{g}}\int_0^{\frac{\pi}{2}}du=\frac{\pi}{2}\sqrt{\frac{l}{g}}.\]

Apa yang kita temukan dari semua matematika rumit ini? Bahwa periode ayunan \(T\) dari sebuah pergerakan pendulum adalah

\[T=2\pi\sqrt{\frac{l}{g}}.\]

Ini menarik karena dari perhitungan ini, pergerakan pendulum tidak bergantung dari seberapa besar sudut tempat kita menjatuhkan pendulum, tapi hanya bergantung the akselerasi gravitasi dan panjang tali pendulum.

Hal ini lah yang juga ditemukan oleh Galileo, dan dia menyebutnya sebagai isokroni pendulum (dari kata iso atau sama dan kroni atau waktu) dimana sebuah pendulum bisa memiliki periode yang sama walaupun dilepas dari sudut yang berbeda.

Jujurly, ini nggak sepenuhnya akurat sih. Kalo kita perhatikan pergerakan pendulum dari berbagai sudut inisial \(\theta_0\), kita dapat melihat bahwa nggak ada isokroni sama sekali! ⁴

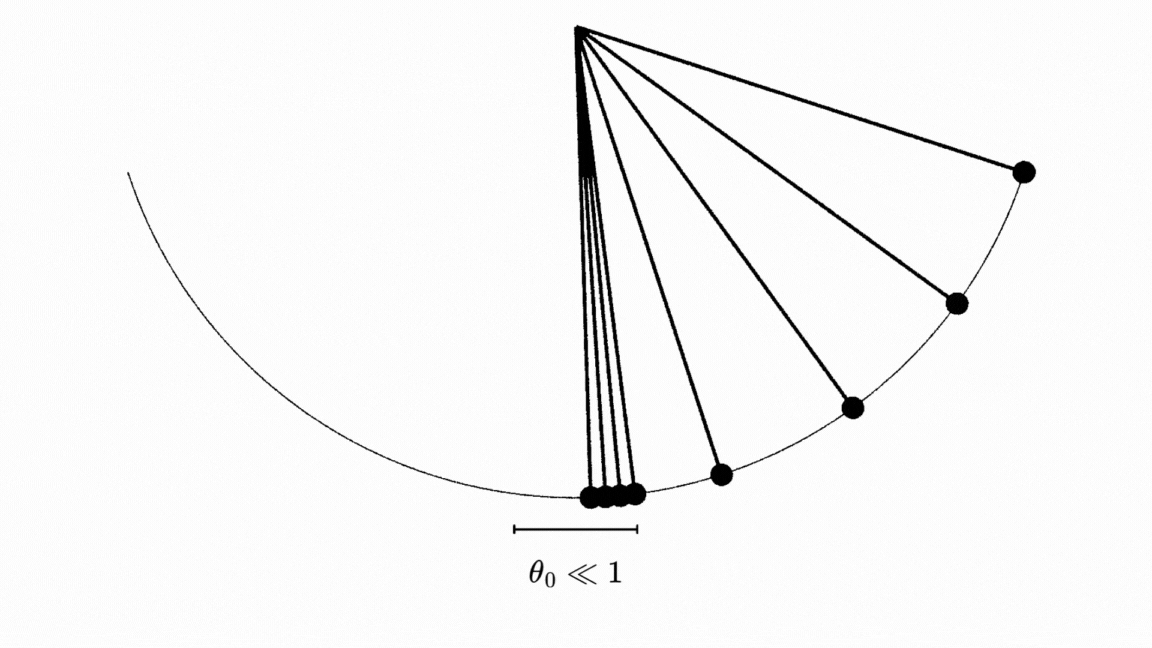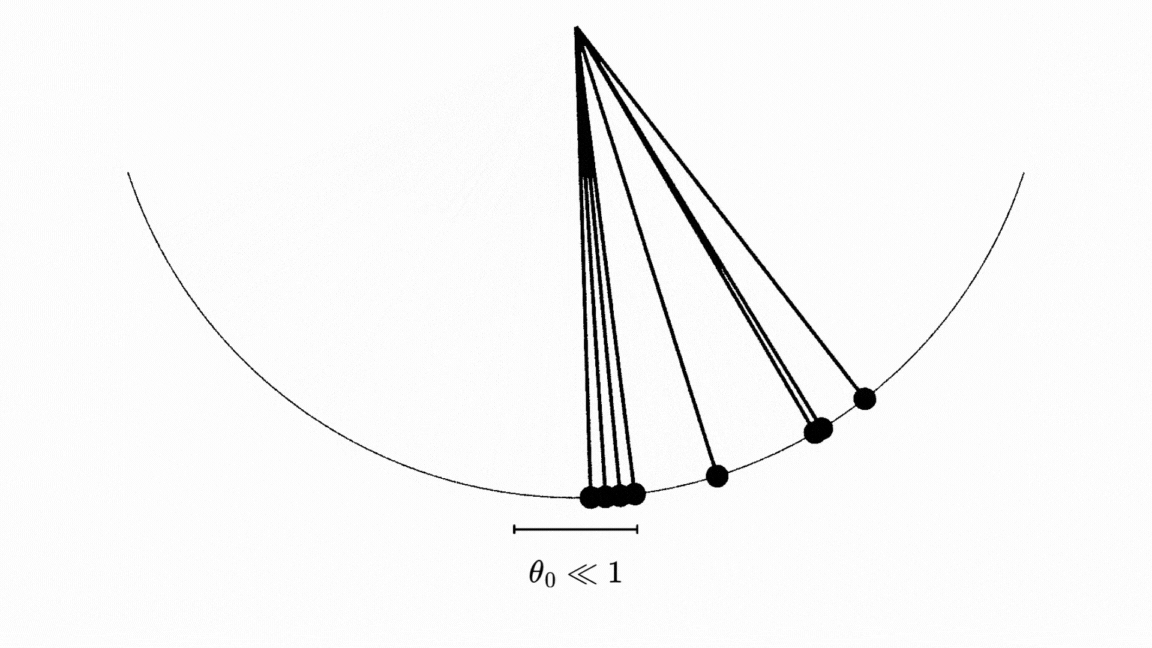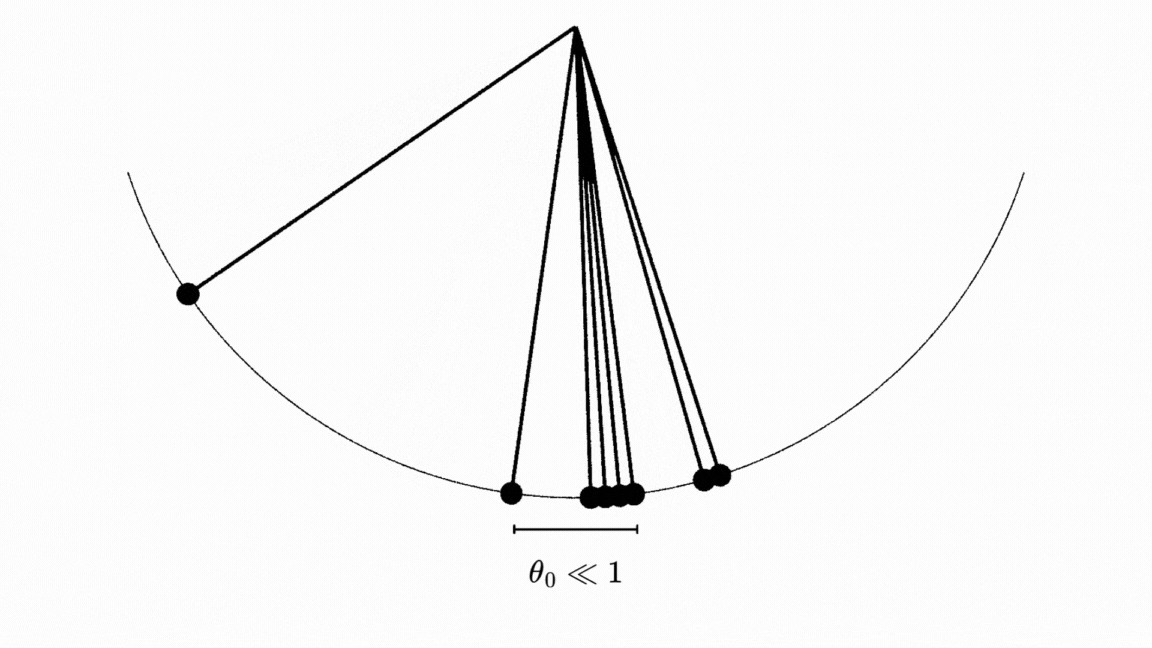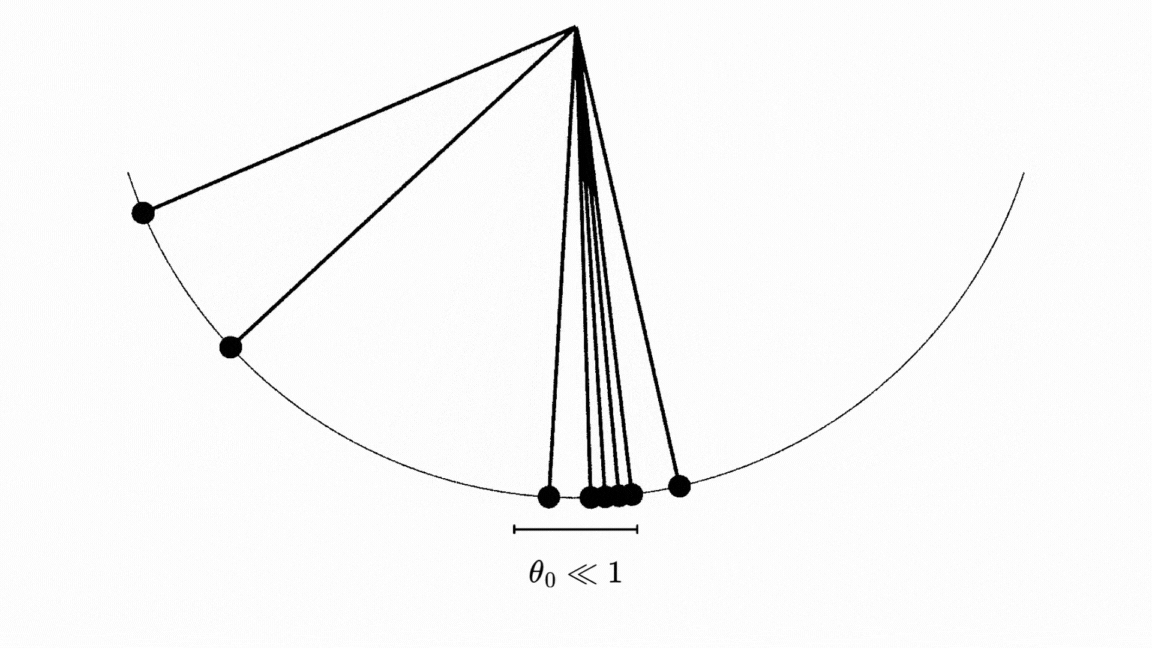
Loh kok bisa? Ini karena sesuai dengan aproksimasi yang kita ambil dari teorema Taylor, kita berasumsi bahwa sudut inisial \(\theta_0\) dekat dengan \(0\). Kalau kalian perhatikan gambar diatas, semua pendulum yang dijatuhkan dari sudut yang besar nggak menunjukkan isokroni sama sekali.

Galileo pun melihat hal yang sama, dan itupun menjadi alasan kenapa sampai sekarang kalo kamu lihat jam pendulum, itu selalu besar dan tinggi, karena untuk mendapatkan ayunan yang akurat, satu-satunya cara adalah dengan membuat tali pendulum yang lebih panjang.

Berhubung pemerintah Belanda berupaya untuk menggunakan jam untuk penjelahan di kapal yang kadang terjal dan penuh gerakan. Hilangnya isokroni di pendulum pada sudut besar menjadi tantangan terbesar Galileo untuk membuat jam akurat.

Galileo terkejar oleh waktu (dan gereja Vatikan)

Sayangnya, hingga ajalnya pada tahun \(1642\), Galileo belum sempat menyelesaikan desain jam pendulumnya. Kerjaannya sempat dilanjutkan oleh anaknya Vincenzio, tapi dia pun dikejar oleh waktu tujuh tahun kemudian 😢.

Untungnya, selama tahun-tahun terakhirnya, ia telah diperkenalkan dengan seorang penyair bernama Constantijn Huygens untuk membantunya berkomunikasi dengan pemerintah Belanda selama keberlangsungan konflik-nya dengan Vatikan ². Constantijn sendiri memiliki empat anak, Christiaan, Constantijn, Philips, dan Susanna.

Yang mengejutkannya, anak pertama Constantijn, Christiaan, pada akhirnya juga menempuh karir sebagai astronom ternama, dan menerima tantangan membuat jam akurat, sama seperti Galileo. Tidak ada bukti kalau komunikasi antara Constantijn dan Galileo telah mempengaruhi keputusan Christiaan untuk menempuh karir di sains, tapi korespondensi antara keluarga Huygens dan Galileo seakan menjadi estafet simbolis untuk menyelesaikan tantangan mengukur waktu.

To be continued…

Referensi